Desigualdades
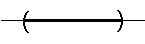


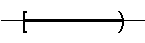
Definición 5.2
Definición 5.3
$\left(a ,+\infty\right)=\big\{x \in\mathbb{R} \mid x \succ a\big\}$
El ordenamiento de $\mathbb{R}$, se lleva a cabo a través de las relaciones denotadas por los símbolos $\prec$; $\succ$; $\leq$ y $\geq$ que significan "menor que"; "mayor que"; "menor o igual que" y "mayor o igual que" respectivamente.
Sean $\ x,\,y,\,z,\,\in \mathbb{R}$
Definición 1.
- $x\prec y \Leftrightarrow y-x\succ 0 $
- $x\succ y \Leftrightarrow x-y\succ 0 $
Definición 2.
- $x\leq y\Leftrightarrow x\prec y \vee x=y$
- $x\geq y\Leftrightarrow x\succ y \vee x=y$
Definición 3.
Los enunciados $\prec$; $\succ$; $\leq$ y $\geq$, se denominan desigualdades.
Definición 4. Desigualdad contínua.
- $x\prec y\prec z\Leftrightarrow x\prec y \wedge y\prec z$
- $x\leq y\leq z\Leftrightarrow x\leq y \wedge y\leq z $
- $x\prec y\leq z\Leftrightarrow x\prec y \wedge y\leq z$
- $x\leq y\prec z\Leftrightarrow x\leq y \wedge y\prec z$
Definición 5.
- $a\succ 0\Leftrightarrow a\in \mathbb{R}^+$
- $a\prec 0\Leftrightarrow a\in \mathbb{R}^-$
Las siguientes propiedades se enuncian sin demostración y son consecuencia inmediata de la propiedad de orden.
Intervalos.
Los siguientes subconjuntos de \mathbb{R}, se denomina Intervalos.
Supóngase $ a,\,b,\,\in \mathbb{R}$ y $a\succ b$
Definición 1.
Llamaremos intervalo abierto y lo denotado por (a, b), al siguiente conjunto:$(a,b)=\left\{ x\in \mathbb{R}/a\prec x\prec b \right\}$
Definición 2
Llamaremos intervalo cerrado de extremos a y b y lo denotado por [a, b], al siguiente conjunto:$[a,b]=\left\{ x\in \mathbb{R}/a\leq x\leq b \right\}$
Definición 3
Llamaremos intervalo semi-abierto por la izquierda, al siguiente conjunto denotado por (a, b]:$(a,b]=\left\{ x\in \mathbb{R}/a\prec x\leq b \right\}$
Definición 4
Llamaremos intervalo semi-abierto por la derecha al siguiente conjunto denotado por [a, b):$[a,b)=\left\{x\in \mathbb{R}/a\leq x\prec b \right\}$
Los símbolos "más infinito o infinito positivo"$+\infty$ y $-\infty$ "menos infinito o infinito negativo", no se debe confundir con números reales.
Definición 5.1
$ \big(-\infty, b\big)= \big\{x \in R\mid x \prec b\big\}$
$ \big(-\infty, b\big)= \big\{x \in R\mid x \prec b\big\}$
Definición 5.2
$ \left(-\infty, b\right]=\big\{x \in\mathbb{R} \mid x \preceq b\big\}$
Definición 5.3
$\left(a ,+\infty\right)=\big\{x \in\mathbb{R} \mid x \succ a\big\}$
Definición 5.4
$\left[a ,+\infty\right)=\big\{x \in\mathbb{R} \mid x\geq a\big\}$
Definición 5.5
$(-\infty ,+\infty)= \mathbb{R} $
Solución de desigualdades.
Llamamos solución de una desigualdad de variable real x, al conjunto de todos los números reales que, al reemplazarlos en la desigualdad la convierte en una proposición verdadera.
A diferencia de las ecuaciones, cuya solución, en general es un número o quizá un conjunto finito de números, el conjunto solución, de una desigualdad consta por lo común de:
- Un intervalo,
- Unión infinita de intervalos y
- En algunos casos el conjunto vacío.
Por ejemplo:
- El conjunto solución de la desigualdad $x^{2}-x\prec 6$, es el intervalo $\left(-2,\, 3 \right)$.
- El conjunto solución de la desigualdad $x^{2}-x\geq 6$,es el intervalo $\left(-\infty, -2 \right]\bigcup \left[3, +\infty \right)$.
- El conjunto solución de la desigualdad $x^{2}+5 = 4$, es el conjunto vacío.
Para resolver desigualdades se deben utilizar las propiedades de orden , considerando los siguientes aspectos:
- Se puede sumar (restar) la misma cantidad en ambos miembros de una desigualdad.
- Se puede multiplicar (dividir) ambos miembros de la desigualdad por una misma cantidad positiva y se mantiene el sentido de la misma.
- Se puede multiplicar (dividir) ambos miembros de la desigualdad por una misma cantidad negativa y se invierte el sentido de la misma.